9.15 For any positive integer n, we can construct a binary tree of n elements as follows:
at level 0, there will be 1 element (the root);
at level 1, there will be 2 elements;
at level 2, there will be 3 elements;
at level 3, there will be 4 elements;
at level 4, there will be 5 elements;
. . .
At the level farthest from the root, there will be just enough elements so the entire tree will have n elements.
For example, if n = 12, we can construct the following tree
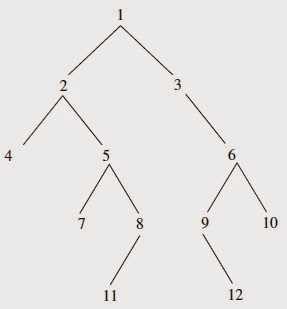
Provide a ! estimate of the height as a function of n.
Hint: Since ! is just an estimate, we can ignore the elements at the lowest level. We seek an integer h such that
1 + 2 + 3 + 4 + . . . + (h + 1) = n
See Example A2.1 in Appendix 2.
Note: This exercise is contrived but, in fact, the ! estimate of the average height of a binary tree is the same as the answer to this exercise (see Flajolet, [1981]).